3D Non-Reflecting Boundary Condition
Non-physical reflections of steady or unsteady flow waves at the far-field (inlet and outlet) can affect the accuracy of a flow simulation. A non-reflecting boundary condition should allow all outgoing waves to exit the flow domain at the far-field boundary without reflection. RPMTurbo has developed an exact three-dimensional non-reflecting boundary condition for steady and unsteady flow simulations.
Unsteady Aerodynamic Modes at Far-field
The key to applying a correct non-reflecting boundary condition is the determination of the unsteady aerodynamic modes at the far-field. RPMTurbo's non-reflecting boundary condition calculates these unsteady modes by numerically solving an eigen problem for the semi-discretized flow equations on a two-dimensional mesh at the inlet and outlet. Unlike previous methods, this method is valid for non-uniform swirling flow. The non-reflecting boundary condition is applied by decomposing the unsteady flow perturbations at the far-field into separate independent waves (unsteady aerodynamic modes). The velocity of each wave is determined and the waves are labeled as incoming or outgoing. The amplitude of the incoming waves are set to zero, except for those that may have been prescribed at the boundary. The outgoing waves are extrapolated out of the domain. It is important that each wave is correctly extrapolated out of the domain to ensure that reflections do not occur.
Paper
RPMTurbo presented a paper on the non-reflecting boundary condition at the 2010 Turbo Expo.
Acoustic Test Case
The 3D non-reflecting boundary condition has been validated by examining an internationally recognized acoustic test case.
Flutter Test Case
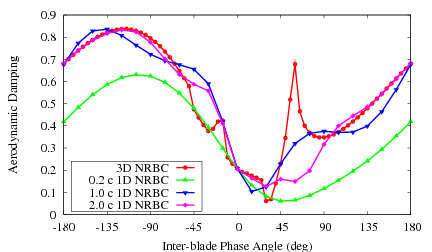
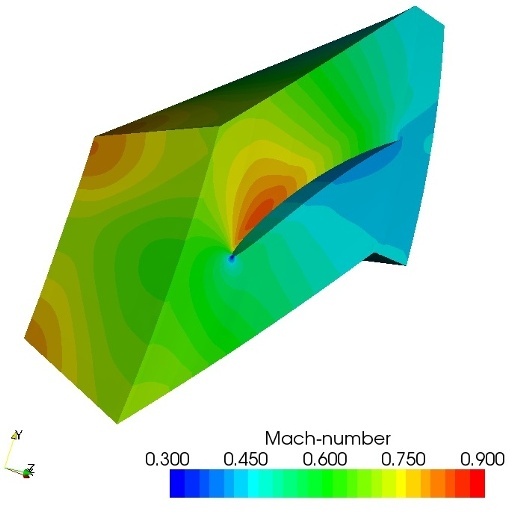
RPMTurbo's 3D non-reflecting boundary condition has been tested on a flutter test, namely the 3D Standard Configuration 10. The aerodynamic damping due to a torsion mode was calculated on three meshes with the inlet and outlet at different locations: 0.2, 1.0 and 2.0 chords from the leading and trailing edge respectively. The steady flow solution on the short domain (0.2 chord) is shown below.
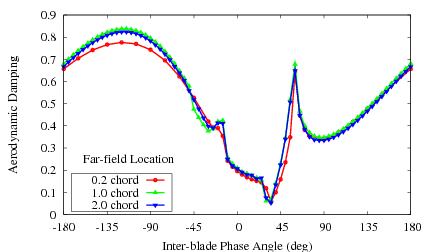
The aerodynamic damping calculated with the 3D non-reflecting boundary condition is shown in the plot below. The three solutions agree well and the solutions are independent of the location of the far-field. This demonstrates that the boundary condition is working correctly.
The aerodynamic damping calculated with a 1D non-reflecting boundary condition is shown in the plot below. The three solutions do not agree and the solutions are dependent on the location of the far-field. The solution calculated with the 3D non-reflecting boundary condition is also shown. It is interesting to note that the agreement with the 3D boundary condition becomes worse as the far-field location is closer to the blade edge. This highlights the importance of applying a 3D non-reflecting boundary condition when using short flow domains.