Specialists in Linear Flow Analysis
CAA Benchmark Problem Category 4
| Geometry | 3D Annulus |
|---|---|
| Number of Blades | 24 |
| Incoming Circumferential Wave Number | 16 |
| Case | 4 |
| Tip Mach Number (Wake) | 0.783 |
| Radial Phase Shift Parameter | 0 |
| Far-field Resolution | 25 x 25 |
Acoustic Modes
The axial wave numbers of the acoustic modes as calculated by the three-dimensional non-reflecting boundary condition are shown below. If the imaginary component of the wave number is zero then the mode is cut-on, that is, the amplitude of the mode does not decay as it propagates in the annulus.
| m | μ | Axial Wave Number | Cut On or Off | Mode Shape | |
|---|---|---|---|---|---|
| Real | Imag | ||||
| -8 | 0 | 5.401 | -3.04e-03 | ON | [Plot] |
| -8 | 1 | 3.502 | -2.10e-02 | ON | [Plot] |
| -8 | 2 | 2.203 | -2.859 | OFF | [Plot] |
| -8 | 3 | 2.215 | -5.062 | OFF | [Plot] |
| 16 | 0 | 2.201 | -3.327 | OFF | [Plot] |
| 16 | 1 | 2.201 | -5.510 | OFF | [Plot] |
| 16 | 2 | 2.197 | -6.991 | OFF | [Plot] |
| 16 | 3 | 2.215 | -8.120 | OFF | [Plot] |
| -32 | 0 | 2.219 | -9.506 | OFF | [Plot] |
Acoustic Mode Plots
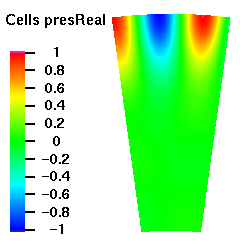
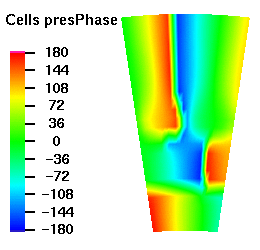
Below are plots of the acoustic mode shapes at the inlet as determined by the 3D non-reflecting boundary conditions. The real part of the pressure perturbation of the mode shape is shown on the left side and the phase of the pressure perturbation on the right side.
Acoustic Mode m=-8 μ = 0
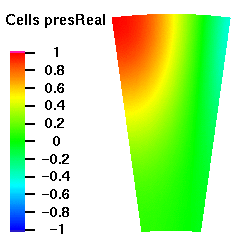
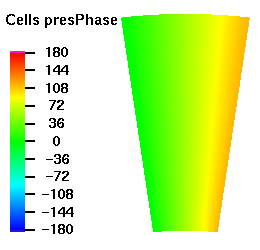
Acoustic Mode m=-8 μ = 1
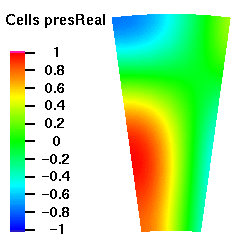
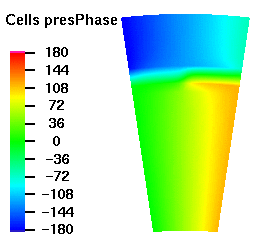
Acoustic Mode m=-8 μ = 2
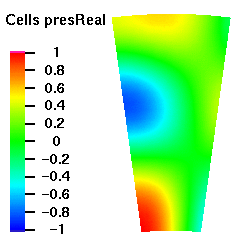
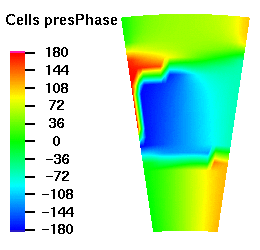
Acoustic Mode m=-8 μ = 3
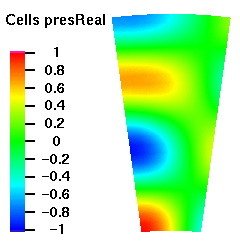
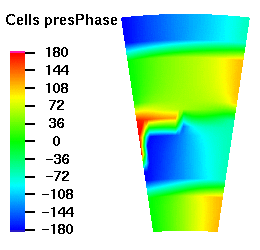
Acoustic Mode m=16 μ = 0
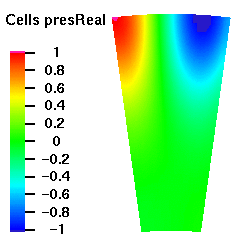
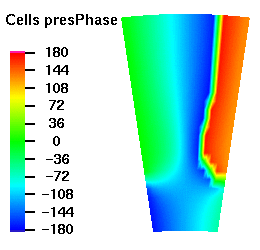
Acoustic Mode m=16 μ = 1
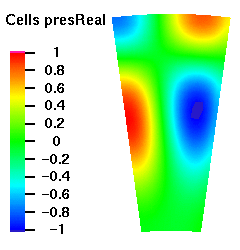
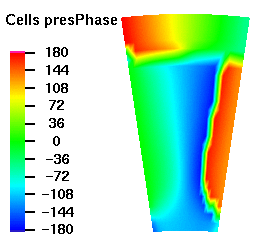
Acoustic Mode m=16 μ = 2
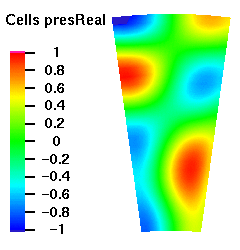
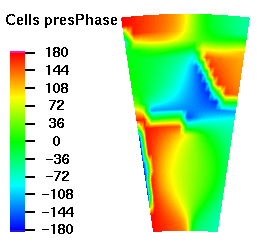
Acoustic Mode m=16 μ = 3
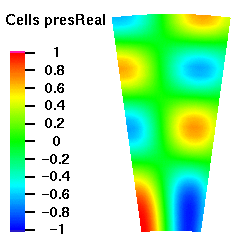
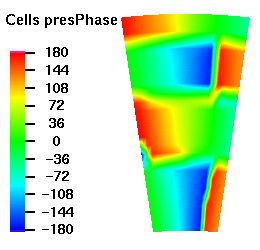
Acoustic Mode m=-32 μ = 0