RPMTurbo
Specialists in Linear Flow Analysis

3D Steam Turbine Flutter Test Case

Introduction

The geometry and steady flow conditions of this test case is the same as the Durham University Open 3D steam test case. This geometry was chosen because it is the only open 3D geometry for a steam turbine stage that we are aware of. The scale of the geometry and prescribed flow conditions are similar to a typical working steam turbine. To create a flutter test case we have simply defined the material of the rotor blade to be steel and it is assumed that the rotor blade is fixed rigidly to the hub.

Geometry

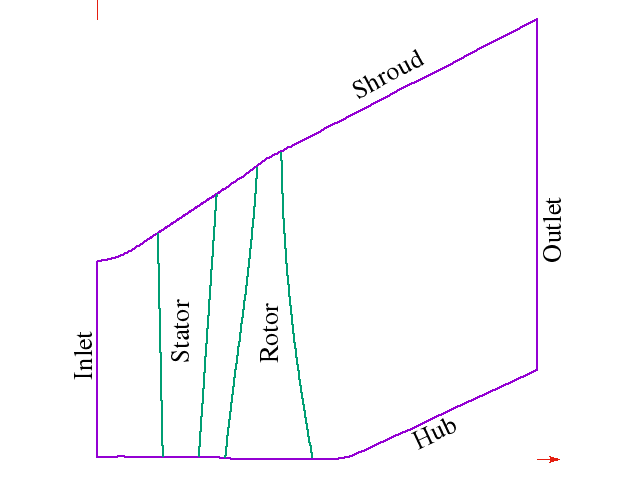
The geometry of the test case consists of a stator and rotor row. The main parameters describing the two rows are listed in the table below. The exhaust geometry is defined by the hub and shroud line in the file Durham_Stage_Test_Case.IGS.

Geometry
Number stator blades 60
Number rotor blades 65
Length rotor blade 920 mm
Speed of rotor 3000 RPM
Stagger angle at tip of rotor 67 deg.
Inlet hub radius 720 mm
Inlet shroud radius 1305.56 mm
Outlet hub radius 979 mm
Outlet shroud radius 2033.6 mm

Download geometry in IGES format (zipped)

Flow Boundary Conditions

The prescribed inlet condition for the stator are listed in the file below. All flow condtion are in SI units (metres, Pascal and Kelvin). The flow angles are in degree. The inletAlpha is the atan (circumfertial velocity component / axial velocity component) and inletBeta is the asin (radial velocity component / magnitude of velocity). The average inlet flow conditions are total pressure 27 kPa and total temperature 340 K, and the average isentropic exit Mach number is 1.12. These conditions are typical for the last stage of steam turbines. The flow is transonic at the rotor tip. We have decided to set a constant static pressure 8800 Pa at the diffuser exit. The turbulence intensity is set to 10% at the inlet of the stator and the rotor.

Download inlet flow boundary conditions

Blade Motion

The geometry defined for this test case is the hot or the aerodynamic geometry. This is the geometry of the blade when the rotor is spinning at 3000 RPM and with the aerodynamic forces at the prescribe operating point. In order to correctly calculate the mode shape we need to calculate the cold geometry, that is the geometry when the rotor is not spinning and without aerodynamic loads.

The blade is assumed to be a free standing blade made from steel which is rigidly fixed at the root. The properties of the steel are shown in the table below.

Density (kg/m^3) 7750
Young's Modulus (GPa) 210.0
Poisson's ratio 0.3

The rotor speed is 3000 RPM. The blade geometry in the IGES files above is the hot geometry. In order to properly calculate the mode shape it is necessary to determing the cold geometry. This can be done iteratively. Pre-stress and spin softening are both considered in the modal calculation. The flutter analysis is performed for the first bending mode. The natural frequency of this modal shape calculated by ANSYS is 92.953 Hz, which correspond to a reduced frequency of 0.2.

The data file for the calculated mode shape of the first bending mode is below. This mode shape was used for all unsteady flow simulations. The mode shape has been normalized so that U^T M U = I. The average kinetic energy of the blade in one cycle is 0.25 omega **2, where omega is the circular frequency when the blade is oscillating at the normalized amplitude.

Download First Bending Mode

Post Processing

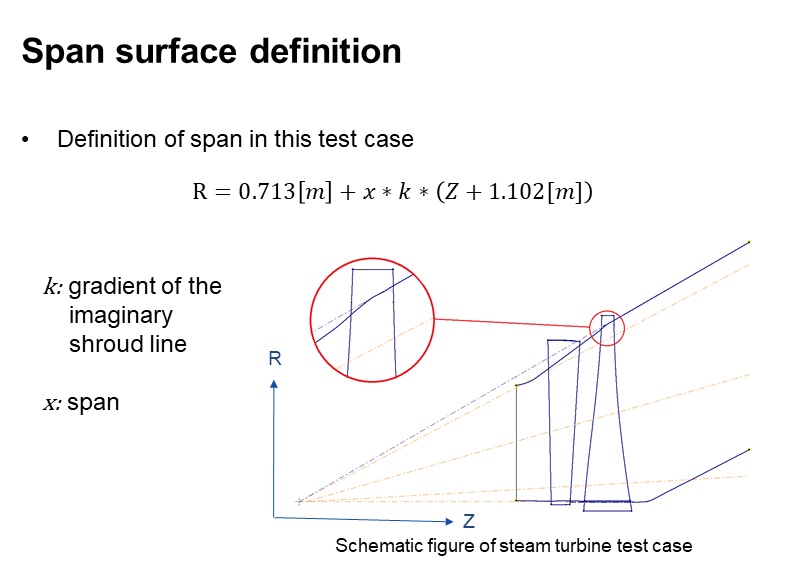
In order to compare solutions from different codes, a consistent method of extracting solutions is required. Solutions are usual compared at a fixed span height. The location of the span surface for a give span percentage is shown in the figure below. The gradient of the shroud is assumed to be k = 0.577.

Meshes

Four meshes created by RPMTurbo are available to download. The first mesh is for URANS flow with the height of the first cell on the walls is 30 microns. The maximum cell aspect ratio for the URANS mesh is 1717. The other three meshes are for inviscid flow calculations with the exit for the rotor domain at different locations. Each mesh has three rows: stator, rotor and exhaust, except for the inviscid long mesh which does not have a separate exhaust domain. Each row is stored in separate zones. The meshes are unstructured hexahedral cells stored in cgns files. The tip gap is not included in the meshes. The minimum cell angles are 27.18, 41.0 and 60.1 degrees for the stator, rotor, and exhaust domains respectively.

Flow URANS inviscid inviscid inviscid
Rotor Domain short short medium long
Cells
stator/rotor/exhaust 		836640 / 908424 / 107184 338922 / 276114 / 60588 338922 / 314262 / 22440 338922 / 336702 / -
Download Mesh urans.cgns inviscidShort.cgns inviscidMedium.cgns inviscidLong.cgns
Domains

More details about the URANS mesh are given below.

Nozzle Rotor Exhaust
Cells 836640 908424 107184
Cells on Hub 10458 13764 1624
Min. Angle (deg.) 27.18 41.57 60.12
Max. Aspect Ration 679.8 1716.7 2785
Cell height on blade (mm) 0.03 0.03 --

Steady solutions

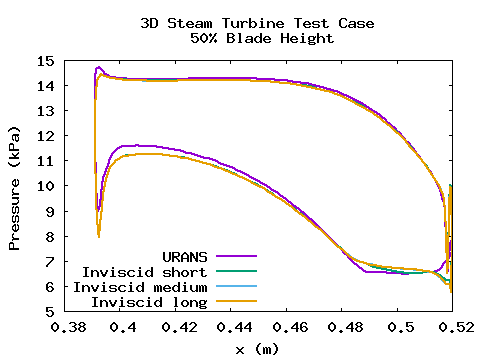
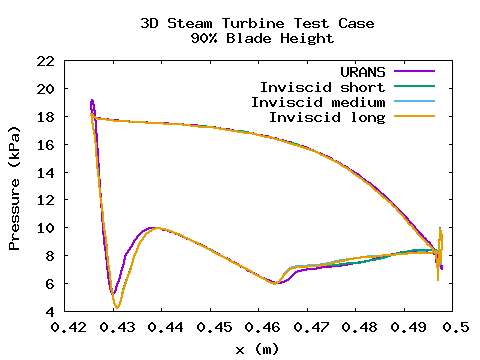
Plots of steady-state pressure on the rotor blade at 50% and 90% span calculated by LUFT on the four meshes are shown below.

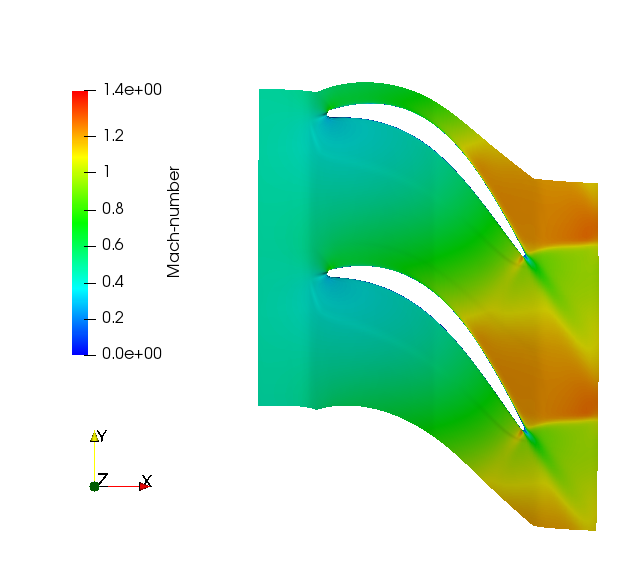
Contour plots of the relative Mach number at 50% and 90% span calculated by LUFT URANS solution are shown below.

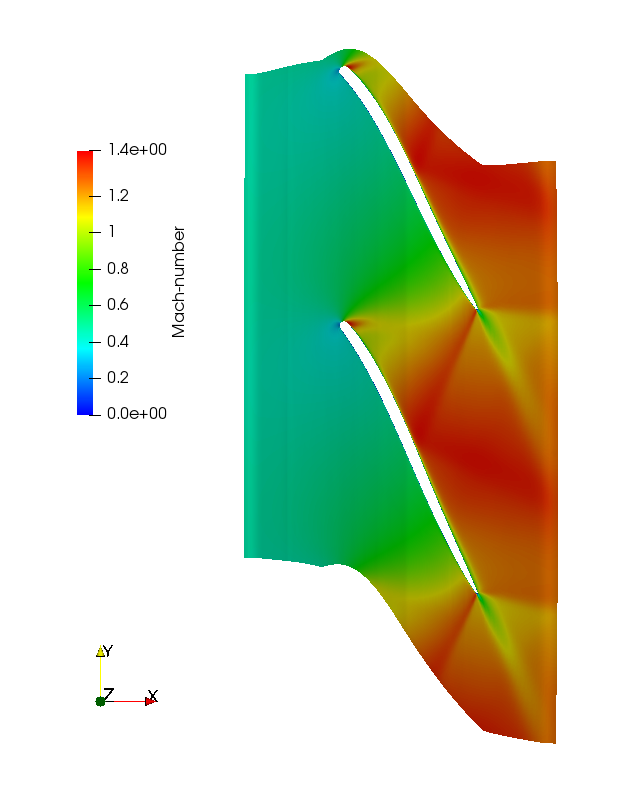
Download LUFT steady-state solutions

Unsteady Solutions

Unsteady flow simulations were performed using LUFT on the rotor domain. The harmonic motion of the blade was prescribed as the first bending mode (data file above) at all possible nodal diameters. The modal frequency was adjusted to 132.08 Hz in order to increase the reduced frequency to 0.3 which is typical for steam turbines in use. The plot of aerodynamic damping versus nodal diameter calculated by LUFT on the four meshes is shown below. The damping curves are very similar for all meshes. This demonstrates that RPMTurbo's non-reflecting boundary condition is work well as the solution is independent of the location of the outlet boundary.

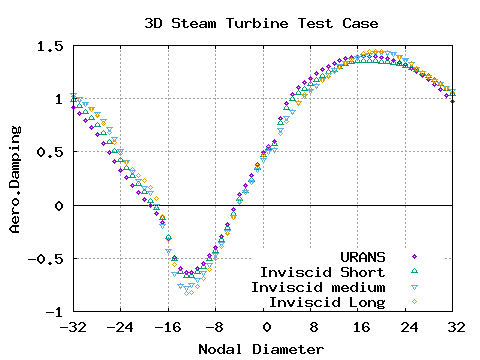
Download LUFT URANS aerodynamic damping data

The unsteady work coefficient at 90% span for nodal diameter d=-13 is shown below.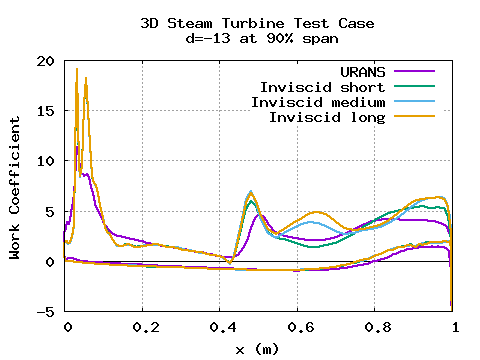

Download LUFT URANS solution at 90% span for d=-13

The unsteady work coefficient on suction (left and pressure (right) side of the blade for nodal diameter d=-13 is shown below.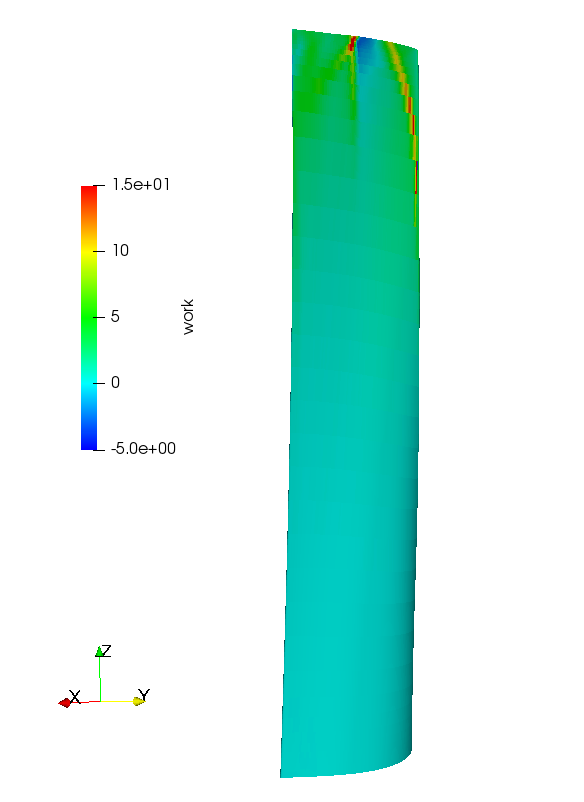

Transonic Dip

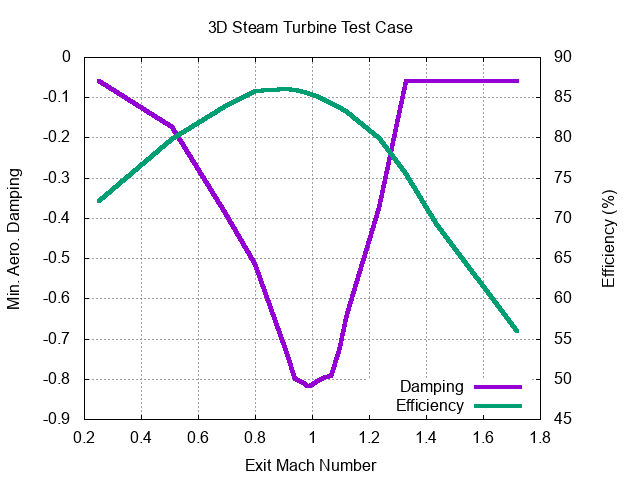
The transonic flutter dip for aircraft wings is well known but it also occurs for steam and gas turbines. The plot below shows minimum aerodynamic damping as a function of exit Mach number for the steam turbine flutter test case. The minimum aerodynamic damping was calculated for twenty operating points. The operating points were varied by changing the exhaust exit pressure. The exit Mach number is the relative isentropic Mach calculated from the exit pressure and average relative total pressure at the turbine inlet. The calculations were run on the inviscid medium rotor mesh. The aerodynamic damping is lowest when the flow is transonic. The stage efficiency is also plotted.

Publications